Chapter 5 Complete Block Designs ANOVA and Mixed Models
Table Of Content

In this design, you would have exactly two of each type of dough in each of the oven runs. You are studying how bread dough and baking temperature affect the tastiness of bread. And let's say you're purchasing packaged bread dough from some food company rather than mixing it yourself. Here is a concise answer.A lot of details and examples might be found in most documents treating the design of experiments; especially in agronomy.
Video 2: Blocking Examples
Blocking can also be understood as replicating an experimenton multiple sets, e.g., different locations, of homogeneous experimental units,e.g., plots of land at an individual location. The experimental units shouldbe as similar as possible within the same block, but can be very differentbetween different blocks. This design allows us to fully remove thebetween-block variability, e.g., variability between different locations, fromthe response because it can be explained by the block factor. In that sense, blocking is a so-calledvariance reduction technique. The use of blocking in experimental design has an evolving history that spans multiple disciplines. The foundational concepts of blocking date back to the early 20th century with statisticians like Ronald A. Fisher.
Blocking used for nuisance factors that can be controlled
We consider an example which is adapted from Venables and Ripley (2002), the original source isYates (1935) (we will see the full data set in Section 7.3). Atsix different locations (factor block), three plots of land were available.Three varieties of oat (factor variety with levels Golden.rain, Marvellousand Victory) were randomized to them, individually per location. Typical block factors are location (see example above), day (if an experiment isrun on multiple days), machine operator (if different operators are needed forthe experiment), subjects, etc. Often, the researcher is not interested in the block effect per se, but he only wants to account for the variability in response between blocks. Of note, the block effect is typically considered as a random effect. Finally, if you expect the 'treatment effect' to differ from block to block, then interactions should be considered.
Example Problem on Randomized Complete Block Design
More specifically, blocking is used when you have one or more key variables that you need to ensure are similarly distributed within your different treatment groups. A matched pairs design is an experimental design where pairs of participants are matched in terms of key variables, such as age or socioeconomic status. One member of each pair is then placed into the experimental group and the other member into the control group. Independent measures design, also known as between-groups, is an experimental design where different participants are used in each condition of the independent variable. This means that each condition of the experiment includes a different group of participants.
Extraneous variables (EV)
First the individual observational units are split into blocks of observational units that have similar values for the key variables that you want to balance over. After that, the observational units from each block are evenly allocated into treatment groups in a way such that each treatment group is allocated similar numbers of observational units from each block. Blocking is one of those concepts that can be difficult to grasp even if you have already been exposed to it once or twice. Because the specific details of how blocking is implemented can vary a lot from one experiment to another. For that reason, we will start off our discussion of blocking by focusing on the main goal of blocking and leave the specific implementation details for later.
The Design Structure has one factor (oven run, Run), and the Treatment Structure two factors (Recipe and Temperature). Because every run has to be a single (nominal) temperature, Temperature and Run must occur at the same level of the experimental design. So far we have discussed experimental designs with fixed factors, that is, the levels of the factors are fixed and constrained to some specific values. In some cases, the levels of the factors are selected at random from a larger population. In this case, the inference made on the significance of the factor can be extended to the whole population but the factor effects are treated as contributions to variance. In general, we are faced with a situation where the number of treatments is specified, and the block size, or number of experimental units per block (k) is given.
Blocking involves grouping experimental units based on levels of the nuisance variable to control for its influence. Randomization helps distribute the effects of nuisance variables evenly across treatment groups. The flow field pattern is crucial in many aspects such as cost-efficiency (in terms of excessive fuel consumption), water management on the cathode side, and achieving a high cell performance. The studies on the reconnaissance of much more effective flow field design have been continuing for years. As a matter of fact, it may be succeeded with some manipulations on the flow area.
2 Data Exploration
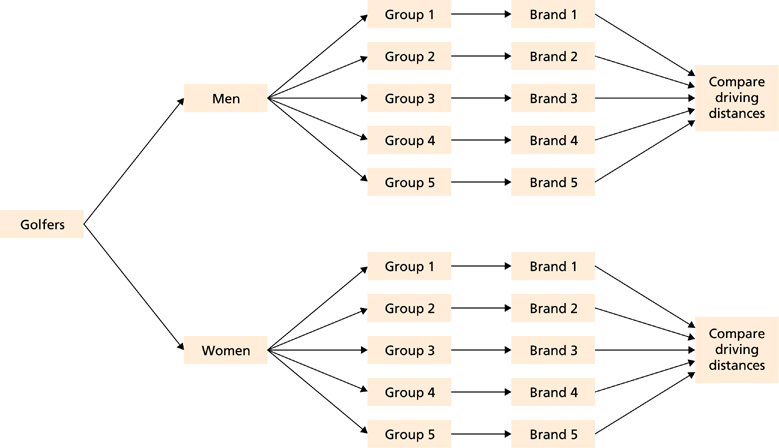
They were given the same passage of text to read and then asked a series of questions to assess their understanding. To compare the effectiveness of two different types of therapy for depression, depressed patients were assigned to receive either cognitive therapy or behavior therapy for a 12-week period. When in doubt, decide on the number of blocks based on previous literature.

Repeated Measures design is also known as within-groups or within-subjects design. This should be done by random allocation, ensuring that each participant has an equal chance of being assigned to one group. The primary interest is the treatment effect in any RCBD, therefore the hypothesis for the design is statistically written as.
atelier FCJZ conceives 'jiading mini-block' as an urban experiment - Designboom
atelier FCJZ conceives 'jiading mini-block' as an urban experiment.
Posted: Fri, 13 Nov 2020 08:00:00 GMT [source]
We could select the first three columns - let's see if this will work. Click the animation below to see whether using the first three columns would give us combinations of treatments where treatment pairs are not repeated. However, this method of constructing a BIBD using all possible combinations, does not always work as we now demonstrate. If the number of combinations is too large then you need to find a subset - - not always easy to do. However, sometimes you can use Latin Squares to construct a BIBD. As an example, let's take any 3 columns from a 4 × 4 Latin Square design.
The contrasts looking at recipe and recipe by dough non-additivity (interaction) do not have run-to-run variability in them. Technically, this is called variously a split-plot design structure or a repeated-measures design structure. Since \(\lambda\) is not an integer there does not exist a balanced incomplete block design for this experiment. Seeing as how the block size in this case is fixed, we can achieve a balanced complete block design by adding more replicates so that \(\lambda\) equals at least 1. It needs to be a whole number in order for the design to be balanced. Here we have treatments 1, 2, up to t and the blocks 1, 2, up to b.
We cannot fit a more complex model, includinginteraction effects, here because we do not have the corresponding replicates. Hence, a block is given by a locationand an experimental unit by a plot of land. In the introductory example, a blockwas given by an individual subject. Why is it important to make sure that the number of soccer players running on turf fields and grass fields is similar across different treatment groups? In this article we tell you everything you need to know about blocking in experimental design. First we discuss what blocking is and what its main benefits are.
A Latin Square design blocks on both rows and columnssimultaneously. If we ignore the columns of a Latin Square designs, the rows form anRCBD; if we ignore the rows, the columns form an RCBD. Here we have two pairs occurring together 2 times and the other four pairs occurring together 0 times. Therefore, this is not a balanced incomplete block design (BIBD). Randomized Complete Block Design (RCBD) is arguably the most common design of experiments in many disciplines, including agriculture, engineering, medical, etc. In addition to the experimental error reducing ability, the design widens the generalization of the study findings.
This subset of columns from the whole Latin Square creates a BIBD. The principle of random allocation is to avoid bias in how the experiment is carried out and limit the effects of participant variables. Note, that the analysis where we ignore that we have multiple technical repeats for each bio-repeat returns results that are much more significant because we act as if we have much more independent observations. Note, that the power is slightly different because for the power.t.test function we conditioned on the mice from our study. While in the simulation study we generated data for new mice by simulating the mouse effect from a normal distribution. \(\rightarrow\) This reduces the variance of the residuals and leads to a power gain if the variability between mice/blocks is large.
To assess the effectiveness of two different ways of teaching reading, a group of 5-year-olds was recruited from a primary school. Their level of reading ability was assessed, and then they were taught using scheme one for 20 weeks. To assess the difference in reading comprehension between 7 and 9-year-olds, a researcher recruited each group from a local primary school.
This kind of design is used to minimize the effects of systematic error. If the experimenter focuses exclusively on the differences between treatments, the effects due to variations between the different blocks should be eliminated. This website is using a security service to protect itself from online attacks. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data. The next thing you need to do after you determine your blocking factors is allocate your observations into blocks. To simplify things, we will assume that you have one main blocking factor that you want to balance over.
Comments
Post a Comment